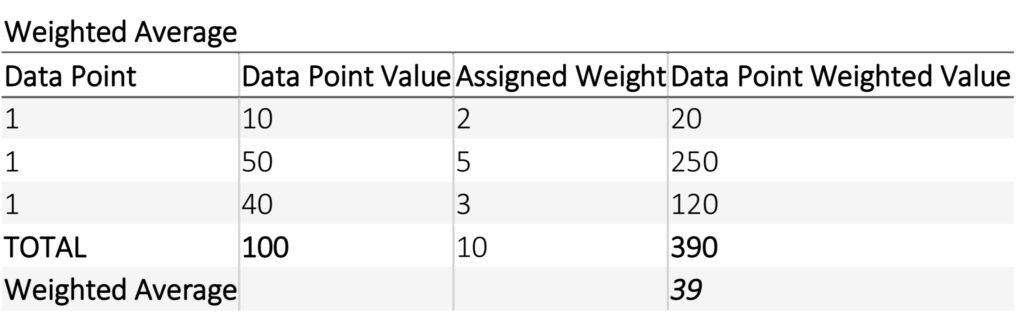
WEIGHTED AVERAGE
The weighted average is a calculation that takes into account the varying degrees of importance of the numbers in a data set. In calculating a weighted average, each number in the data set is multiplied by a predetermined weight before the final calculation is made. A weighted average can be more accurate than a simple average in which all numbers in a data set are assigned an identical weight.
Weight average also called weighted mean is helpful to make a decision when there are many factors to consider and evaluate. Each of the factors is assigned some weights based on their level of importance, and then the weighted average is calculated using a mathematical formula. The weighted average assigns certain weights to each of the individual quantities. weights do not have any physical units and are only numbers expressed in percentages, decimals, or integers. The weighted average formula is the summation of the product of weights and quantities, divided by the summation of weights
Weighted Average=∑(Weights×Quantities) / ∑Weights
KEY TAKEAWAYS
1) The weighted average takes into account the relative importance or frequency of some factors in a data set.
2) A weighted average is sometimes more accurate than a simple average.
3) Stock investors use a weighted average to track the cost basis of shares bought at varying times.
4) In calculating a simple average, or arithmetic mean, all numbers are treated equally and assigned equal weight. But a weighted average assigns weights that determine in advance the relative importance of each data point.
5) A weighted average is most often computed to equalize the frequency of the values in a data set. For example, a survey may gather enough responses from every age group to be considered statistically valid, but the 18-34 age group may have fewer respondents than all others relative to their share of the population. The survey team may weight the results of the 18-34 age group so that their views are represented proportionately.
However, values in a data set may be weighted for other reasons than the frequency of occurrence. For example, if students in a dance class are graded on skill, attendance, and manners, the grade for skill may be given greater weight than the other factors.
In any case, in a weighted average, each data point value is multiplied by the assigned weight which is then summed and divided by the number of data points. In a weighted average, the final average number reflects the relative importance of each observation and is thus more descriptive than a simple average. It also has the effect of smoothing out the data and enhancing its accuracy.
How does a weighted average differ from a simple average?
A weighted average accounts for the relative contribution, or weight, of the things being averaged, while a simple average does not. Therefore, it gives more value to those items in the average that occur relatively more.
How is a weighted average calculated?
You can compute a weighted average by multiplying its relative proportion or percentage by its value in sequence and adding those sums together. Thus if a portfolio is made up of 55% stocks, 40% bonds, and 5% cash, those weights would be multiplied by their annual performance to get a weighted average return. So if stocks, bonds, and cash returned 10%, 5%, and 2%, respectively, the weighted average return would be (0.55 x 10%) + (0.40 x 5%) + (0.05 x 2%) = 7.6%.
Examples of Weighted Averages
Weighted averages show up in many areas of finance besides the purchase price of shares, including portfolio returns, inventory accounting, and valuation. When a fund that holds multiple securities is up 10 percent on the year, that 10 percent represents a weighted average of returns for the fund with respect to the value of each position in the fund.
For inventory accounting, the weighted average value of inventory accounts for fluctuations in commodity prices, for example, while LIFO (Last In First Out) or FIFO (First In First Out) methods give more importance to time than value.1 When evaluating companies to discern whether their shares are correctly priced, investors use the weighted average cost of capital (WACC) to discount a company's cash flows. WACC is weighted based on the market value of debt and equity in a company's capital structure.
A few real-life examples would help us better understand this concept of weighted average. A teacher evaluates a student based on the test marks, project work, attendance, and class behavior. Further, the teacher assigns weights to each criterion, to make a final assessment of the performance of the student. The image below shows the weight of all the criteria that help the teacher in her assessment. The average of the weights helps in showing a clear picture.

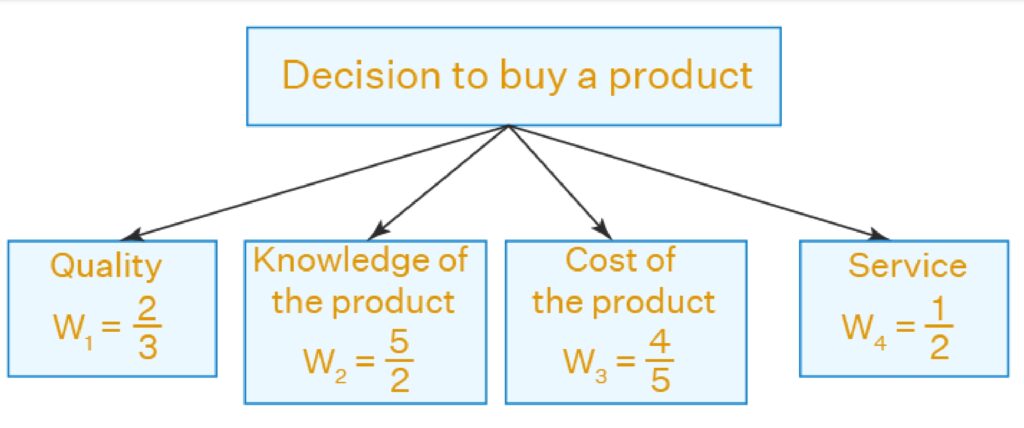
A customer's decision to buy or not to buy a product depends on the quality of the product, knowledge of the product, cost of the product, and service by the franchise. Further, the customer assigns weight to each of these criteria and calculates the weighted average. This will help him in making the best decision while buying the product.
Basic concepts on averages
1)An average or more accurately arithmetic mean can be defined as the sum of n different data divided by n.
2) The average of a group is defined as the ratio of sum of all the items in the group to the number of items in the group.
3) Average = (Sum of all items in the group)/ Number of items in the group
Find the Average Speed
~If a person travels a distance at a speed of x km/hr and the same distance at a speed of y km/hr then the average speed during the whole journey is given by-
~If a person covers P km at x km/hr and Q km at y km/hr and R km at z km/hr, then the average speed in covering the whole distance is- {(P+Q+R) / ( [P/x] + [Q/y] + [R/z] ) }
When a person leaves the group, and another person joins the group in place of that person then-
~If the average age is increased: Age of new person = Age of separated person + (Increase in average × total number of persons)
~If the average age is decreased: Age of new person = Age of separated person – (Decrease in average × total number of persons)
When a person joins the group-
~In case of increase in average: Age of new member = Previous average + (Increase in average × Number of members including new member)
~In case of decrease in average: Age of new member = Previous average – (Decrease in average × Number of members including new member)
~Average of n natural no’s=(n+1)/2
~Average of even No=(n+1)
~Average of odd No= n
~General Formula = (1st number +Last number)/2
QUESTION 1
Sid wants to purchase a mobile phone and checks on the internet and finds a rating of 8/10 for features and 7/10 for durability. Based on his requirement Sid gives a weightage of 60% to features and 40% for durability. How can you help Sid calculate the final rating for the mobile phone?
Solution:
The final rating of the mobile phone can be calculated using the concept of weighted average.
Rating for features = 8/10 and rating for durability = 7/10
Weight for features = 60% and weight for durability = 40%
Weighted
Average=60%×810+40%×710=0.6×0.8+0.4×0.7=0.48+0.28=0.76=7.610Weighted
Average=60%×810+40%×710=0.6×0.8+0.4×0.7=0.48+0.28=0.76=7.610
Therefore, the final rating of the mobile is 7.6/10.
QUESTION 2
In a 50 over cricket match, the average runs scored by a team for different sessions of the innings are given below. Find the average runs scored by the team in that innings.
First ten overs - 8 runs per over
10 to 35 overs – 5 runs per over
Last 15 overs – 9 runs per over
Solution:
To find: Average runs scored.
Given: Total overs = 50
w1 = 8
w2 = 5
w3 = 9
x1 = 10
x2 = 25
x3 = 15
Now, to find the sum of weighted terms, multiply the average runs scored in the respective session and then add them up.
Sum of weighted terms = w1 × x1 +w2 × x2 + w3 × x3 = 8(10) + 5(25) + 9(15) = 80 + 125 +
135 = 340
Now, using the weighted average formula,
Weighted Average = Sum of weighted terms/Total number of terms
= 340/50
= 6.8
Therefore, the average runs scored in that innings by the team = 6.8.
QUESTION 3
In a group of 10 students, the mean of the lowest 9 scores is 42 while the mean of the highest 9 scores is 47. For the entire group of 10 students, the maximum possible mean exceeds the minimum possible mean by.
Solution:
Here a2 to a9 is common to both the terms
So, a1 + (a2 to a9) = 42 × 9
a10 + (a2 to a9) = 47 × 9
Solving these two a10 – a1 = 45
a1, a2, a3,……………, a9, (a1 + 45)
One instance is every number is 42
42, 42, …………………, 42, 42+45 (a1 to a9 are equal) ———–(1)
Another instance is every number is 47
47 – 45, 47, …………………, 47, 47 (a2 to a10 are equal) ———(2)
Mean of (1) = 46.5
Mean of (2) = 42.5
1. – (2) = 4
QUESTION 4
Ramesh and Gautam are among 22 students who write an examination. Ramesh scores 82.5.The average score of the 21 students other than Gautam is 62. The average score of all the 22 students is one more than the average score of the 21 students other than Ramesh. The score of Gautam is [CAT 2019]
Solution
Let the score of Gautam =x
Total marks of all the students = 21*62 +x
As per question The average score of all the 22 students is one more than the average score of the 21 students other than Ramesh,
Or (21*62 +x)/22 -1 = (21*62 +x – 82.5)/21
(21*62 + x -22)/22 = (21*62 +x – 82.5)/21
On solving x =51

